[LeetCode]打家劫舍合集

简单整理一下LeetCode上打家劫舍系列题目, 该系列作为状态机动态规划的入门题相当的好.

打家劫舍

题目描述

有一行非负数, 不能选连续两个数, 求选的数之和的最大值.

思路

整体思路上使用状态机的思路解决.

• 状态机关心的是当前处于何种状态, 所有可能的状态转移方式与条件.

• 结合本题, 我们使用状态机动态规划解决本题.

• 动态规划

  • 状态定义:
    1. $f[i][0]$表示考虑了前i个数, 且不拿i号位置的情况下取得的最大价值
    2. $f[i][1]$表示考虑了前i个数, 且拿i号位置的情况下取得的最大价值
  • 状态转移:
    1. 若不拿i号位置, 则i - 1位置可拿可不拿, 因此$f[i][0] = max(f[i - 1][0], f[i - 1][1])$
    2. 若拿i号位置, 则i - 1位置必不能被拿, 因此$f[i][1] = f[i - 1][0] + nums[i]$

• 最后的答案为$max(f[n][0], f[n][1])$

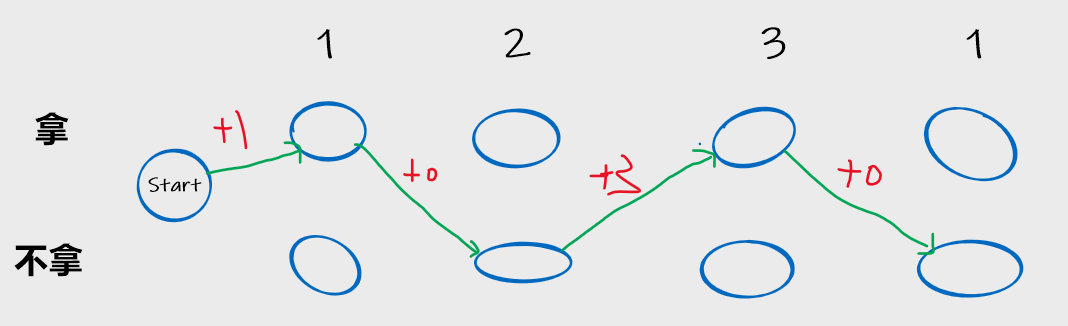
• 任何一种拿与不拿的决策, 均对应于有限状态机中不同状态之间的一条转移边.

Code

// 上述解法
class Solution {
public:
    int rob(vector<int>& nums) {
        int n = nums.size();
        vector<vector<int>> f(n + 1, vector<int>(2, 0));
        for (int i = 1; i <= n; i ++ ) {
            f[i][0] = max(f[i - 1][0], f[i - 1][1]);
            f[i][1] = f[i - 1][0] + nums[i - 1];
        }
        return max(f[n][0], f[n][1]);
    }
};

复杂度分析

• 时间复杂度$O(N)$
• 空间复杂度$O(N)$(注意到当前状态只依赖于上一位置状态, 因此可以使用两个变量保存上一位置状态, 优化成$O(1)$)

---

打家劫舍 II

题目描述

基本题意与第一题类型, 只不过多了一个限制: 首尾不能同时拿.

思路

依照第一题的思路, 我们继续使用状态机动态规划解决. 只不过需要多一维的状态, 用于指示1号位置是否被拿, 因为这关系到最后一个位置的转移条件.

• 动态规划
  • 状态定义:
    1. $f[i][0][0]$表示i号位1号位都没拿.
    2. $f[i][0][1]$表示i号位没拿, 1号位拿了.
    3. $f[i][1][0]$表示i号位拿了, 1号位没拿.
    4. $f[i][1][1]$表示i号位1号位都拿了.
  • 状态转移：
    1. 对于$f[i][0][0]$, 则$i - 1$位无限制, 因此$f[i][0][0] = max(f[i - 1][1][0], f[i - 1][0][0])$.
    2. 对于$f[i][0][1]$, 则$i - 1$位无限制, 因此$f[i][0][1] = max(f[i - 1][1][1], f[i - 1][0][1])$.
    3. 对于$f[i][1][0]$, 则$i - 1$位不能选, 因此$f[i][1][0] = f[i - 1][0][0] + nums[i - 1]$.
    4. 对于$f[i][1][1]$, 则$i - 1$位不能选, 因此$f[i][1][1] = f[i - 1][0][1] + nums[i - 1]$.
       对于i = n: 由于1号位和n号位不能同时选, 因此转移需要单独考虑.

Code

class Solution {
public:
    int rob(vector<int>& nums) {
        int n = nums.size();
        vector<vector<vector<int>>> f(n + 1, vector<vector<int>>(2, vector<int>(2, 0)));
        f[1][1][1] = nums[0];
        for (int i = 2; i < n; i ++ ) {
            f[i][0][0] = max(f[i - 1][1][0], f[i - 1][0][0]);
            f[i][0][1] = max(f[i - 1][1][1], f[i - 1][0][1]);
            f[i][1][0] = f[i - 1][0][0] + nums[i - 1];
            f[i][1][1] = f[i - 1][0][1] + nums[i - 1];
        }
        // 单独考虑n号位
        f[n][0][0] = max(f[n - 1][1][0], f[n - 1][0][0]);
        f[n][0][1] = max(f[n - 1][1][1], f[n - 1][0][1]);
        f[n][1][0] = f[n - 1][0][0] + nums[n - 1];
        return max({f[n][0][0], f[n][0][1], f[n][1][0]});
    }
};

/*
  这里简单提一下另外一种做法, 类似于第一题.
  考虑到 1 和 n 不能同时被拿, 因此最优解有以下可能
    1. 拿1不拿n
    2. 拿n不拿1
    3. 1和n不拿
  因此可以考虑在1 -> n - 1上和 2 -> n上分别使用第一题的解法做一遍.
  因为求解的是最大值, 这两个子问题有所重复的无所谓的(他们都包含第三种情况), 只需不遗漏的计算所有可能即可.
*/
class Solution {
public:
    int rob(vector<int>& nums) {
        int n = nums.size(), ans = 0;
        if (n == 1) return nums.back();
        vector<vector<int>> f(n + 1, vector<int>(2, 0));
        // 1 -> n - 1
        for (int i = 1; i < n; i ++ ) {
            f[i][0] = max(f[i - 1][0], f[i - 1][1]);
            f[i][1] = f[i - 1][0] + nums[i - 1];
        }
        ans = max({ans, f[n - 1][0], f[n - 1][1]});
        // 2 -> n
        f[1][0] = f[1][1] = 0;
        for (int i = 2; i <= n; i ++ ) {
            f[i][0] = max(f[i - 1][0], f[i - 1][1]);
            f[i][1] = f[i - 1][0] + nums[i - 1];
        }
        return max({ans, f[n][0], f[n][1]});
    }
};

复杂度分析

• 时间复杂度$O(N)$
• 空间复杂度$O(N)$

---

打家劫舍 III

思路

状态机结合树形动态规划的题目.使用树形动态规划解决.

• 树形动态规划
  • 状态定义:
    1. $f[u][0]$表示考虑以u为根的子树中, 且u没被选的情况下最大价值.
    2. $f[u][1]$表示考虑以u为根的子树中, 且u被选的情况下最大价值.
  • 状态计算
    1. 对于$f[u][0]$, 由于没有拿父节点u, 因此对于任意子节点v, 都可以考虑拿他和不拿他, 因此有转移:
       $$
       f[u][0] = \sum_{v \in son[u]}max(f[v][0], f[v][1])
       $$
    2. 对于$f[u][1]$, 由于拿了父节点u, 因此对于任意子节点v, 都不能拿他, 因此有转移:
       $$
       f[u][1] = \sum_{v \in son[u]} f[v][0]
       $$

       Code

       /**
        * Definition for a binary tree node.
        * struct TreeNode {
        *     int val;
        *     TreeNode *left;
        *     TreeNode *right;
        *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
        *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
        *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
        * };
        */
       class Solution {
       public:
           unordered_map<TreeNode*, vector<int>> f;
           void dfs(TreeNode* u) {
               f[u] = vector<int>(2, 0);
               f[u][1] = u -> val;
               for (auto& son : {u -> left, u -> right}) {
                   if (son == nullptr)
                       continue;
                   dfs(son);
                   f[u][0] += max(f[son][0], f[son][1]);
                   f[u][1] += f[son][0];
               }
           }
           int rob(TreeNode* root) {
               dfs(root);
               return max(f[root][0], f[root][1]);
           }
       };

       复杂度分析

• 时间复杂度$O(N)$: DFS过程中, 每个节点只会被遍历一次
• 空间复杂度$O(N)$

---

参考资料

• B站yxc

---

欢迎讨论指正